Rydberg atoms in Quantum Technologies

When a single valence electron of an atom is excited to a state of high principal quantum number n (greater than 10) it behaves like a highly excited electron in a hydrogen atom. An atom in such a state is known as a Rydberg atom. Rydberg atoms are suitable for use in quantum technologies like quantum computing, electromagnetic field sensing, and quantum optics. The following are a few properties that render them this suitability: The electron is far from the nucleus, hence it is weakly bound. Moreover, highly-excited Rydberg states are metastable with long lifetimes, which can be orders of magnitude longer than the low-lying excited states. Also, the large number of available energy levels and their separations allow coupling to electromagnetic fields. As a result, Rydberg atoms are extremely sensitive to nearby atoms or to the electromagnetic field in the microwave and terahertz region.

Many useful properties, such as the polarizability, energy levels, level spacing, radiative lifetime of the atom, and so on, scale strongly with n. The strong scaling with n occurs because the binding energy of the electron becomes weaker with increase in n. The core of the Rydberg atom is an electrostatic trap for a weakly bound electron which can be strongly perturbed by an applied electric field. Atomic interactions are very strong in Rydberg atoms and can be tuned by selecting states with different principal quantum numbers.

Recent efforts to develop quantum technology are motivated by the fact that precisely manipulating systems at a quantum level offers particular advantages over classical techniques. Due to these properties, Rydberg atoms are one of the most tunable quantum systems and are highly desirable for developing new quantum technologies. The strong interactions between nearby Rydberg atoms make them suitable for use as quantum simulators or in quantum computing. Quantum simulation and computing is done using ultra-cold Rydberg atoms in optical tweezer arrays. The sensitivity of Rydberg atoms to microwave or terahertz fields make them ideal sensors of electromagnetic fields in these regions.

Rydberg atoms also have applications in non-linear quantum optics, including light-matter interfaces - single photon sources and photon gates. The lifetime of the Rydberg states is an important factor because the lifetime can put a limit on the coherence time of the Rydberg state, thus, determining the feasibility of some experiments.

Rydberg atoms in Quantum Computation:

Quantum computers offer a platform to simulate quantum systems such as molecules or some materials, as well as solving classically hard problems ranging from factorisation to optimisation problems such as logistics or network optimisation.

Using Rydberg atoms, a large number of identical and long coherence qubits in arrays of arbitrary geometry and dimensionality can be used for both digital and analog quantum computation. One of the requirements for quantum information processing is the ability to prepare high-fidelity states and perform readout as well as achieving long coherence times in the computational basis.

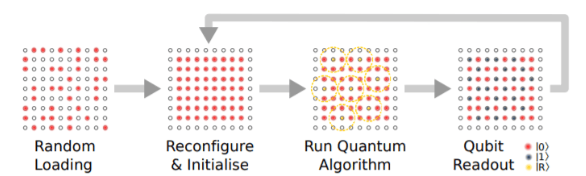
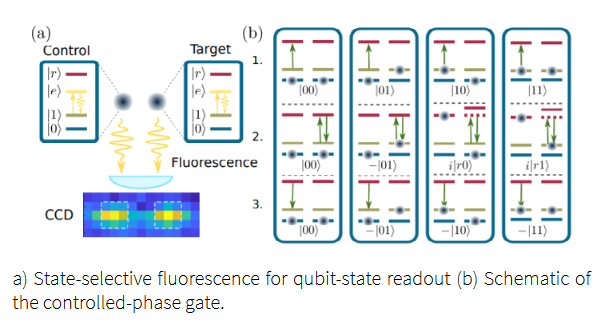
A Rydberg array quantum computer (Fig1) is composed of atoms which are initially loaded stochastically. A defect free qubit register is achieved by rearrangements of these atoms. Coherent excitation to Rydberg states allows implementation of quantum algorithms exploiting long-range interactions to couple neighbouring qubits. Digital quantum computing utilises a series of sequential gates applied onto a qubit register followed by a state-selective measurement to project atoms into the |0> and |1> logical output states. For qubits separated within 10 µm, the strong dipole-dipole interactions induce a conditional excitation process that allows a controlled phase-gate to be applied. This gate requires three laser pulses as shown in Fig 2b, first a π-pulse on the control qubit followed by a 2π-pulse on the target qubit. If the control qubit is in state |r> then blockade detunes this pulse from resonance on the target qubit and no phase is acquired, however if the control is in state |0> then the target executes a complete rotation and acquires a phase shift of exp(iπ). A final pulse returns the control qubit to |1> leading to the realisation of a controlled phase gate.

The Rydberg array platform can also be used as an effective analog quantum simulator for spin models. These provide a simplified many-body Hamiltonian described highly-correlated condensed matter systems. Researchers are aiming to achieve higher fidelity manipulations and increase the output quality of these gates and provide internal error corrections. Trapped ions, superconductors, Bose-Einstein condensates are few others which are used in quantum computing.

REFERENCES

1) Adams C.S., Pritchard J.D., Shaffer J.P (2020); “Rydberg atom quantum technologies”, Journal of Physics B: Atomic, Molecular and Optical Physics,53(1),art.no.012002

2) M. Saffman, T.G Walker, K. Molmer (2010); “Quantum information with Rydberg atoms”, Rev. Mod. Phys. 82, 2313

3) Igor I Ryabtsev, Denis B Tretyakov and Ilya I Beterov(2005); “Applicability of Rydberg atoms to quantum computers” J. Phys. B: At. Mol. Opt. Phys. 38

4) https://physicsworld.com